Compton Saçılması
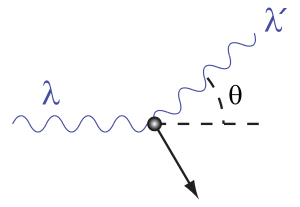
Kısaca: Compton olayı (veya Compton saçılması), yüksek enerjili X ışınlarının fotonu ile karbon atomunun serbest elektronunun çarpıştırılması sonucu elektronun ve fotonun şekildeki gibi saçılması olayıdır. 20. yüzyılın başlarında, X-ışınlarının madde ile etkileşimi araştırılmaya devam edildi. ...devamı ☟
Compton dalga boyu
3 yıl önceCompton dalgaboyu bir parçacığın kuantum mekaniği özelliğidir. Compton dalgaboyu Arthur Compton tarafından elektronların foton saçılması olayı izah edilirken...
Foton
3 yıl önceNobel Fizik Ödülü'nü kazandırmıştır). Daha sonra Arthur Compton tarafından açıklanan Compton saçılması olayı ve Albert Einstein'ın açıkladığı Fotoelektrik...
Foton, Elektromanyetik dalga, Elektron, Elektron Volt, Enerji, Fermiyon, Fizik, Frekans, Graviton, Işık hızı, Kuark, Manyetik, Kuantum fiziği, Einstein, KuantumDavisson-Germer deneyi
3 yıl önceBroglie hipotezini doğruladı. Bu deneyinin sonucunun Arthur Compton'un keşfettiği Compton saçılması deneyinin sonuçları ile birleştirilmesi quantum teorisinin...
X ışını kristalografisi
3 yıl öncetarafından ortaya atılmış, ancak 1922’de Arthur Compton tarafından X-ışınlarının elektronlardan saçılması deneyiyle doğrulanmasına kadar geniş kabul görmemiştir...
Elektron
3 yıl önceçarpışmaya Compton saçılması denir. Bu çarpışma ile parçacıklar arasında momentum ve enerji aktarımı yaşanarak fotonun dalga boyu Compton kayması olarak...
Elektron, Fizik, Fermiyon, Kuark, Molekül Orbital Teorisi, İyon, Proton, Atom, Nötron, Radyoaktif, FotonNobel Fizik Ödülü sahipleri listesi
3 yıl önceçalışmalarından, özellikle çökelme dengesini keşfinden dolayı" 1927 Compton, ArthurArthur Compton ABD "kendi adıyla adlandırılan etkiyi keşfinden dolayı" Wilson...