Türkçe Bilgi logo TürkçeBilgi

Değerleyici Güvenebilirliği

Kısaca: Değerleyici güvenebilirliği, değerleyiciler arasıda uyuşma, veya konkordans değerleyiciler arasında bulunan uyuşma derecesini ölçmek amacı ile kullanılan istatistiksel yöntemleri kapsar. ...devamı ☟

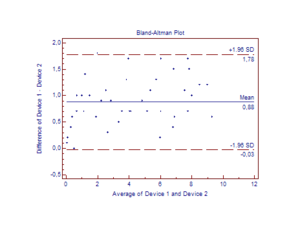
Değerleyici güvenebilirliği
Değerleyici Güvenebilirliği

Değerleyici güvenebilirliği, değerleyiciler arasıda uyuşma, veya konkordans değerleyiciler arasında bulunan uyuşma derecesini ölçmek amacı ile kullanılan istatistiksel yöntemleri kapsar. Bu yöntemlerin amacı yargı mevkiinde olan kişilerin yaptığı sayısal veya sayısala dönüştürülebilir değerlendirmelerde ne kadar hemfikir veye türdeş olduklarına bir sayısal değer bulmaktır. Özellikle aynı konuyu veya konumu değerlendiren insancıl değerleyicileri bu çeşit yargıya varma yeteneklerini geliştirmek ve değerlemelerinin daha da adilane olmasını sağlamak için bu yöntemler çok kullanışlıdır. Eğer belli bir değişkene göre yapılan değerlemelerde uyuşma yoksa ya kullanılan değişken veya seçim yapılabilecek kategoriler listesinde bazı eksiklikler veya hatalar vardır ya da değerleyicilerin yargılarında uyuşmayi iyilestirmek için yeniden veya daha fazla eğitim sağlamak gereği ortaya çıkar. Değerleyiciler arasındaki uyuşmanın ölçülmesi için kullanılan birkaç istatistiksel yöntem bulunmaktadır. Değişik istatistiksel ölçüler değişik tipte ölçülme ölçeğindeki değiskenlerle ilişkilidir. Bazı seçilebilecek istatistiksel ölçüler şunlardır: uyuşma için ortak-olasılık, kappa katsayıları, değerleyiciler arası korelasyon katsayıları, konkordans korelasyon katsayısı ve sınıf içi korelasyion katsayısı. Uyuşma için ortak olasılık

Uyuşma için ortak olasılık

 genellikle en basit ve bu nedenle güçlü ölçme sağlar. Bu ölçüyü hesaplamak için her sayısal değerleme kategorisi, yani değerleme puanı, için (örneğin 1, 2,.. 5) her değerleyicinin vermiş olduğu sayı o değerleme kategorisi için verilmiş olan toplam sayısı ile bölunüur. Bu ölçü verilerin tam olarak isimsel ölçekli olduğunu varsaymaktadır. Değerleyiciler arası uyuşmanın yalnızca rastgeleliğe bağlı olma ihtimalini de hesaba katmamaktadır. Kappa istatistikleri İki değerleyici problemine için uygun olan Cohen'in kappa katsayısı ve bunun değişmiyen sabit çok sayıda değerleyici problemlerine adaptasyonu olan Fleiss'in kappa katsayısı uyuşma için ortak olasılık ölçüsünden daha uygun sonuç verdiği kabul edilir; çünkü değerleyici uyuşmasının sırf rastgelelik dolayısı ile ortaya çıkması da kappa ölçülerine içeriktir. Ancak kappa olçüleri de, yine uyuşma için ortak olasılık ölçüsü gibi verilerin isimsel ölçekli yani kategori puanlarının arasında hiç doğal olarak sırasallık bulunmadığını varsaymaktadırlar. Halbuki pratikte birçok değerlendirme için kabul edilen kategoriler ve verilen puanlar sırasal ölçeklidirler. Korelasyon katsayıları Pearson'un çarpım-moment korelasyon katsayısı r veya Spearman'in sıralama korelasyon katsayısı \rho veya Kendall'ın sıralama korelasyon katsayısı \tau değerleyicileri ikişer ikişer alarak değerlendirme puanları arasındaki doğrusal ilişkiyi bir korelasyon katsayısı olarak bulurlar. Her üç korelasyon katsayısı da -1 ile +1 arasında değişmekte ve eğer iki değerleyici arasında uyuşma varsa +1 yakın olması gerekmektedir. Pearson'un r'si için elemanlar verilen puanların (veya seçilen kategori sayılarının) aralıklı ölçekli veya orantılı ölçekli yani niceliksel olmaları gerekmektedir. Pearson'un r bu türlü ölçekli olduğu kabul edildiği gibi, genel olarak daha fazla çıkartımsal istatistik kullanılacaksa (ornegin r için bir guvenilme araligi kurulacaksa), bu verilerin bir normal dağılım gösteren bir anakütleden geldiği varsayımı olduğu da kabul edilir. Halbuki Spearman'ın \rho'su ve Kendall'ın \tau'sı içinse puanların (veya seçilen kategori sayılarının) sırasal ölçekli olduğu varsayılır. Bu türlü korelasyon katsayıları parametrik olmayan istatistik veya dağılım gösteremeyen istatistik olarak kabul edilmektedir. Dikkat edilirse bu üç değişik korelasyon katsayısı (r, \rho ve \tau) değerleyicileri çift çift karşılaştırmaktadır. Mümkün olan bütün çifter karşılaştırmalar hep birlikte bir korelasyon matrisi halinde ifade edilebilir. Bu korelasyon matrisi çapraza göre simetrik olduğundan yalnız bir üst üçgen veya alt üçgen şekilde gösterebilinir. Ama yine de çok sayıda değerleyici olduğu hallerde bu korelasyon matrisi tum uyuşmayı gösteremez. Eğer ikiden daha çok sayıda değerleyici varsa ve bu çoklu sayıda değerleyici için tek bir konkordans katsayısı bulunmak istenirse bu halde Kendall'in konkordans katsayısı W bulunabilir. Kendall'in W katsayısı için değişme aralığı 0 (hiç uyuşma olmaması) ile 1 (tam olarak uyuşma olması) olur. Kendall'in W katsayısı parametrik olmayan istatistik olduğu için, özellikle verilerin normal dağılım gösterdiği varsayılan Pearson'un çarpım-momenti korelasyon katsayısı r kiyasla, daha güçlü olduğu kabul edilir. Sınıf-içi korelasyon katsayısı Değerleyici güvenebilirliğinin sınanması için bir diğer yöntem de sınıf-içi korelasyon katsayısı hesaplanmasıdır.. Bu katsayı hesaplanması için birkaç değisik formül bulunmaktadır. Bir özel şekildeki formül * bir gözlemin varyansı ile gerçek puanlamanın gözümlenen elamanlar arasındaki değişkenliği ile orantısı olarak tanımlanmaktadır. Bu şekil sınıf-içi korelasyon katsayısı 0.0 ve 1.0 değerleri arasında değişebilmektedir. (Daha önce popüler olarak kullanılan bir diğer şekilde hesaplanan katsayı için değişme aralığı -1 ile +1 olur). Her gözümlenen elamana değerleyiciler tarafından verilen değerleme puanları arasında çok az değişkenlik varsa (yani bütün değerleyiciler ya aynı ya da çok yakın değerleme puanı vermişlerse, sınıf-içi korelasyon katsayısı değeri yüksek (yani '+1'e yakin) olacaktır.

Sınıf-içi korelasyon katsayısı

 hem değerleyiciler arasındaki korelasyonu, ve hem de her bir eleman tabakasının değişik değerlendirilmesi ihtimalini de göz önüne aldığı için Pearson'un r, Spearman'ın \rho ve Kendall'ın \tau korelasyon katsayılarından daha ayrıntılı ve uygun sonuç verdiği kabul edilebilir. Uyuşma için limit Sadece iki degerleyici bulundugu hallerde bir diger degerleyici uyusmasini analiz iki degerleyici arasinda bulunan farklari bulup bu farklarin ortalamasini almakdir. Bu degerleme farklarinin standart sapmasi da bulunarak anakutle ortalama farklari icin bir guven araligi kurmak da mumkun olur. Eger iki degerleyici genellikle uyusmakta iseler ortalama sifira yakin olacaktir. Eger bir degerleyici surekli olarak digerinden degismeyen sekilde devamli fark gosteriyorsa, ortalama sifirdan uzak olacaktir ama guven araligi dar olacaktir. Eger iki degerleyici birbiri ile uyusamuyor ise ama bu uyusmama bir tutarli sekilde degilde gayet rastgele oluyorsa, o zaman ortalama sifir yakininda olabilir ama guven araligi genis olacaktir. Bland ve Altman bu aciklamayi bir ozel gosterim ortaya cikarak daha da genisletmisler. Bu gosterimde her bir eleman icin degerleme farklari gosterilmektedir. Yatay eksen her bir degerlenen eleman dikey eksende iki degerleyicinin arasindaki degerleme puan farki gosterilir; boylece gosterimin icinde her bir eleman icin bir nokta bulkunacaktir. Farklarin ortalamasi bir yatay eksen paralel dogru ortaya cikartir ve bunun ustunde ust guven limiti ve altinda alat guven limit cizilir. Bland-Altman gösterimi bu grafik icinde gosterilen noktalarin bu ortalama etrafinda ve guven limitlerine gore nasil bir gorunum gosterdigini incelemeye yardim eder. Anack bu arastirma cok defe subjektif goruse baglidir. Uyusma olmasi bu nokatalarin ortalama etrafinda ve guven araligi icinde rastgele dagilmasi ile anlasilir. Aralik disina cikan dislak noktalar olup olmadigi, bir belli grup elaman icin belli bir turlu fark olmamasi gibi olagandisi gorunuslerinde olup olmadigi arastirilabilir. Referanslar Dışsal kaynaklar * John Übersax tarafından hazırlanmış değerleyici uyuşması için istatistiksel yöntemler * Online tıp eğitimi için hazırlanmış değerleyici güvenebilirliği hesaplayıcısı

Kaynaklar

Vikipedi