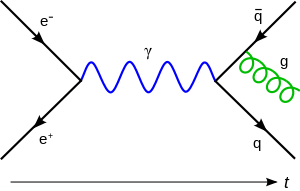
Kuvantum Alan Kuramı
Kısaca: Parçacık alan kuramı (kuvantum alan teorisi), hareketli parçacık sistemlerinin kuantizasyonuyla ilgilenen parçacık mekaniğiyle benzer olarak, alanların hareketli sistemlerine parçacık mekaniğinin uygulamasıdır. ...devamı ☟