Türkçe Bilgi: Kalıntı teoremi

kalıntı teoremi veya bilinen bir diğer adıyla rezidü teoremi, analitik fonksiyonların kapalı eğriler üzerindeki çizgi integrallerini bulmak için kullanılan önemli bir araçtır ve ayrıca sık bir şekilde gerçel integralleri bulmak için de kullanılır. Cauchy integral teoremini ve Cauchy integral formülünü genelleştirir. İfadesi ise şöyledir: U, karmaşık düzlem C 'nin basit bağlantılı açık kümesi, a₁,...,a_n U 'nun sonlu çokluktaki noktaları ve f, U \ üzerinde tanımlı ve holomorf bir fonksiyon olsun. γ, U içinde a_k'yi sınırlayan ancak hiçbirini kesmeyen doğrultulabilir bir eğriyse ve başlangıç noktası bitiş noktasıyla aynıysa, o zaman :

\oint_\gamma f(z)\, dz = 2\pi i \sum_^n \operatorname(\gamma, a_k)  \operatorname( f, a_k )

olur. γ Jordan eğrisi ise, I(γ, a_k) = 1 olur ve böylece :

\oint_\gamma f(z)\, dz = 2\pi i \sum_^n \operatorname( f, a_k )

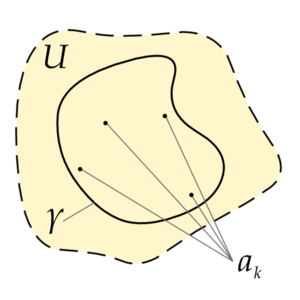
olur. Burada, Res(f, a_k) ifadesi f 'nin a_k 'deki kalıntısını ve I(γ, a_k) ifadesi γ 'nın a_k etrafındaki dolanım sayısını göstermektedir. Dolanım sayısı tamsayıdır ve sezgisel olarak γ 'nın a_k etrafında ne kadar sıklıkla döndüğünü ölçer; γ a_k etrafında saat yönünün tersine dönerse pozitiftir, eğer a_k etrafında γ hiç dönmüyorsa 0'dır. Gerçel integralleri bulmak için, kalıntı teoremi şu şekilde kullanılır. İntegrali alınan ifade karmaşık düzleme genişletilir ve kalıntıları hesaplanır (ki genelde kolaydır). Gerçel eksenin bir kısmına, yukarı yarı düzlemde veya aşağı yarı düzlemde yarım çember eklenerek, eksenin alınan parçası kapalı bir eğri haline getirilir. Genelde, yarım çemberin yarıçapı büyüdükçe integralin yarım çember üzerindeki kısmı sıfıra doğru gider. Bu da sadece gerçel eksen üzerindeki integrali bırakır ki aslında ilgilendiğimiz bu kısımdır. Örnek :

\int_^\infty  \over x^2+1}\,dx

integrali olasılık kuramında Cauchy dağılımının karakteristik fonksiyonunu hesaplarken ortaya çıkar ve basit hesapların tekniğiyle kolayca hesaplanamaz. Gerçel eksen üzerinde -a 'dan a 'ya ve sonra da 0 merkezli bir yarıçember üzerinde a 'dan -a 'ya saat yönünün tersi yönde giden bir kontür boyunca alınan kontür integrallerinin bir limiti olarak ifade ederek bu integrali hesaplayacağız. a 'yı 1'den büyük alalım böylece i sanal sayısı eğrinin içinde olsun. Kontür integrali şudur: :

\int_C \,dz =\int_C  \over z^2+1}\,dz.

e^itz bir tam fonksiyon olduğu için (karmaşık düzlemin hiçbir noktasında tekilliği yoktur), bu fonksiyonun sadece paydanın yani z² + 1 'in sıfır olduğu yerlerde tekillikleri vardır. z² + 1 = (z + i)(z - i) olduğu için bu noktalar sadece z = i veya z = -i olabilir. Bu noktalardan sadece bir tanesi ise bu kontür tarafından sınırlıdır. :} \,\! ||

=\frac}\left(\frac-\frac\right)\,\!

|- | ||

=\frac}\frac+\frac}\left( \frac-1}\right) -\frac} , \,\!

|} olduğu için, f 'nin z = i 'deki kalıntısı :

\operatorname_f(z)=\over 2i}

olur. O zaman, kalıntı teoremine göre, :

\int_C f(z)\,dz=2\pi i\cdot\operatorname_f(z)=2\pi i \over 2i}=\pi e^

olur. C kontürü bir "doğru" parçaya ve eğri yaya ayrılabilir böylece :

\int_}+\int_}=\pi e^\,

ve bu yüzden :

\int_^a =\pi e^-\int_}

olur. Eğer t > 0 ise :

a\rightarrow\infty\ \mbox\ \int_} \over z^2+1}\,dz \rightarrow 0

olduğu gösterilebilir. Bu yüzden, t > 0 ise :

\int_^\infty \over z^2+1}\,dz=\pi e^

olur. i etrafından dolanmak yerine -i etrafından dolanan bir yay için yapılan benzer bir tartışma t < 0 ise :

\int_^\infty \over z^2+1}\,dz=\pi e^t

olduğunu gösterir. Sonuç olarak, :

\int_^\infty \over z^2+1}\,dz=\pi e^

olur. (Eğer t = 0 ise, o zaman integralin sonucu basit hesap yöntemleriyle bulunur ve değeri de π 'dir.) Ayrıca bakınız * Kontür integrali metodları * Morera teoremi * Nachbin teoremi * * * Dış bağlantılar * Kalıntı teoremi MathWorld'de * Kalıntı Teoremi Modülü, John H. Mathews tarafından

Kaynaklar

Vikipedi

Kalıntı Teoremi

Kaynaklar

Kalıntı (karmaşık analiz)

Cebirin Temel Teoremi

Karmaşık Analiz Konuları Listesi

Cauchy integral teoremi

Korunmalı tekillik

Norton Teoremi

Çizgi integrali

Gerçel analiz

Kalıntı Teoremi

Kalıntı Teoremi Hakkında Detaylı Bilgi

Kaynaklar

Görüşler ve Yorumlar

Okuma Önerileri

Kalıntı (karmaşık analiz)

Cebirin Temel Teoremi

Karmaşık Analiz Konuları Listesi

Cauchy integral teoremi

Korunmalı tekillik

Norton Teoremi

Çizgi integrali

Gerçel analiz