Örnek
Karmaşık analizdeki temel sonuçlardan birisi de z-1 in birim çember C etrafındaki (veya 0 etrafındaki herhangi bir Jordan eğrisi boyunca) integralinin 2πi olmasıdır. Şimdi : integralini bulalım. Bu integrali bulmak için, kontür olarak γ(t) = eit, t ∈ 2π ile parametrize edebileceğimiz |z| = 1 birim çemberini kullanıyoruz. γ'(t) = ieit olduğunu gözlemleyip, bunu da z için yerine koyarsak : elde ederiz ki bu da integralin değeridir. İntegral teoremlerinin uygulanması İntegral teoremlerinin uygulanması genelde kontür integrallerini bir kontür boyunca bulmak için kullanılır. Bu da gerçel değerli integralin hesaplanmasının bir kontür integralini hesaplamayla aynı zamanda yapıldığı anlamına gelir. Cauchy integral teoremi veya kalıntı teoremi gibi integral teoremler, genellikle şu yöntemde kullanılır: * Belli bir kontür seçilir: : Kontür seçilir. Öyle ki, kontür karmaşık düzlemin gerçel değerli integrali tanımlayan bir parçasını takip eder ve ayrıca integrandın da tekilliklerini içerir. Böylece, Cauchy integral formülü veya kalıntı teoreminin kullanımı mümkün olur. * Cauchy-Goursat teoreminin uygulanması : İntegral her kutup etrafındaki küçük bir çember etrafında alınan bir integral haline gelir. * Cauchy integral teoremi veya kalıntı teoreminin uygulanması : Bu integral formülünün uygulanması kontürün tümü üzerindeki integralin değerini verir. * Kontürün gerçel ve sanal kısımları olan başka bir kontüre bölünmesi. : Tüm kontür karmaşık düzlemin parçasını takip eden bir integrale bölünür ki bu kontür de daha önce seçilmiş gerçel değerli integrali (buna R diyelim) ve karmaşık düzlemi kesen integrali (buna da I diyelim) açıklar. Tüm kontür üzerinde alınan integral bu parçalanmış her kontür üzerindeki integrallerin bir toplamıdır. * Karmaşık düzlemi kesen integralin gösteriminin toplamda bir rolü yoktur. : Eğer I integralinin sıfır olduğu gösterilebilirse veya aranan gerçek değerli integral düzensiz integral ise ve sonra yukarıdaki gibi açıklanan I integralinin 0'a gittiğini gösterebilirsek, R boyuncaki integral R+I kontürü boyuncaki integrale gidecektir. * Sonuç : Yukarıdaki adımı gösterebilirsek, o zaman R 'yi, gerçel değerli integrali, dolaysız bir şekilde hesaplayabiliriz.Örnek
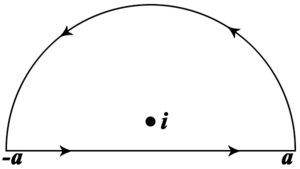
(I) : integralini ele alalım. Bu integrali bulmak için karmaşık değerli, i ve -i noktalarında tekillikleri olan : fonksiyonuna bakıyoruz. Bununla birlikte, gerçel değerli integrali çevreleyecek kontürü de seçmek istiyoruz; böylece solda gösterilen ve uzattığımızda tüm gerçel ekseni içerecek (a sonsuza gidecek) yarım çemberi seçiyoruz. Bu kontüre C diyelim. Şimdi, ilerlemek için kullanabileceğimiz iki adım var: Cauchy integral formülü veya kalıntılar yöntemi. * Cauchy integral teoreminin kullanılması :: :: olduğunu gözlemleyelim. Kontür içindeki tek tekilli i 'deki tekillik olduğu için, :: olur ve bu yüzden : olur. 'Eğer t > 0 ise, o zaman' : Bu yüzden, 'eğer t > 0 ise, o zaman' : i yerine -i 'yi dolanan bir yay durumundaki benzer bir tartışma 'eğer t < 0 ise, o zaman ' : olduğunu gösterir ve sonuç olarak şunu elde ederiz: : ( t = 0 ise, o zaman integral gerçel-değerli hesabın yöntemleriyle çözülebilecek duruma gelir ve değeri de π olur.)Örnek
(III) – trigonometrik integraller Trigonometrik fonksiyonları içeren integrallere belli yerine koymalar yapılarak bu integraller karmaşık değişkenli rasyonel fonksiyonların integrallerine dönüştürülebilir ve böylece yukarıdaki teknikler integrali bulmak için kullanılabilir.Örnek
olarak şu integrali ele alalım: : z = eit yerine koymasını yapabilmeyi arıyoruz. Şimdi, şunları hatırlayalım: : ve : C 'yi birim çember alarak ve yerine koymayı yaparak şunu elde ederiz: : : : : : Cauchy integral formülünü kullanıyoruz. Paydayı çarpanlarına ayıralım: : : : O zaman göz önüne alınması gereken tekillikler 3-1/2i ve -3-1/2i 'de olur. O zaman integral şu hale gelir: : Burada C1, 3-1/2i etrafındaki küçük çemberdir ve C2, -3-1/2i etrafındaki büyük çemberdir. Şimdi formülü uygulayabiliriz: : :: : :: : : : : :Örnek
(IIIa) – trigonometrik integraller, genel prosedür Yukarıdaki yöntem, ve 'nun polinom olduğu : tipindeki bütün integrallere; yani trigonometrik terimler halindeki rasyonel fonksiyonların integrallerine uygulanabilir. Burada yapılan hile , yerine koyması yapmaktır. Bu yüzden : elde edilir. Bu yerine koyma aralığını birim çembere gönderir. Dahası, : ve : olur ve böylece yerine koyma işleminden değişkenli bir rasyonel fonksiyonu ortaya çıkar ve integral : haline gelir ki bu da birim çember içindeki 'nin kalıntılarının toplanmasıyla hesaplanır. Sağdaki resim bunu şimdi hesaplayacağımız : için göstermektedir. Birinci adım şudur: : Yerine koymayla : elde edilir. Bu fonksiyonun kutupları ve 'dedir. Bunlardan ve birim çemberin dışında yer alırken (kırmızı ile gösterilmiştir ancak ölçekli gösterilmemiştir), ve birim çemberin içinde yer alır (mavi ile gösterilmiştir). Karşılık gelen kalıntıların her ikisi de 'ye eşittir böylece integralin değeri : olur.Örnek
(IV) – dallanma kesikleri : integraline bakalım. Şu karmaşık integrali formüle ederek başlayabiliriz: : Yine ilişkin kalıntıları elde etmek için Cauchy integral formülü veya kalıntı teoremini kullanabiliriz. Ancak, burada dikkat edilmesi gereken nokta z1/2=e1/2.Log(z) olmasıdır böylece z1/2 'nin dallanma kesiği vardır. Bu da seçtiğimiz C kontürünü etkiler. Normalde, logaritma dallanma kesiği negatif gerçel eksen olarak tanımlanır; ancak, bu da integralin hesabını biraz daha karışık hale getirir. Bu yüzden, dallanma kesiğini pozitif eksen olarak alıyoruz. O zaman, orijinde ε yarıçaplı bir çemberle başlayan, bu çemberden uzayarak pozitif gerçel eksene oldukça yakın ve paralel olan ancak eksene dokanmayan sonra da saat yönünün tersi yönde ufak çemberden daha büyük yarıçapta bir döngü (neredeyse tam bir çember) yapıp tekrar pozitif eksene parallel bir şekilde (ancak bu sefer negatif eksen yönünde) ufak çemberle birleşen ve anahtar deliği kontürü adı verilen kontürü kullanalım. z = -2 ve z = -4 büyük çemberin içindeler. Bunlar kalan iki kutuptur ve integrandın paydasını çarpanlara ayırarak elde edilebilir. z = 0 'daki kutuptan orijin etrafında tur yapılarak kaçınılmıştır.γ, ε yarıçaplı ufak çember, Γ ise R yarıçaplı büyük çember olsun. O zaman, : z1/2 = e1/2 Log(z) olduğu için, dallanma kesiğinin üzerindeki kontür üzerinde, γ boyunca argumentte 2π kazanılmıştır ( Euler Özdeşliğiyle, birim vektörü temsil eder ki bu yüzden log olarak 'ye sahiptir. z 'nin argumentinden de kastedilen bu 'dir. 1/2 katsayısı ise bizi 2 çarpı yazmaya zorlamaktadır.); böylece : : basitleştirerek, : ve sonra : elde edilir. Γ ve γ üzerindeki her iki integralin de ε sıfıra ve R sonsuza gittikçe sıfıra gittiği yukarıda bir tahmin tartışması yapılarak gösterilebilir. Bu yüzden, o zaman, : Kalıntı teoremi veya Cauchy integral formülü kullanılarak (iki basit kontür integralinin toplamını elde etmek için ilk önce kısmi kesirler yöntemini kullanarak), aşağıdaki elde edilir. :