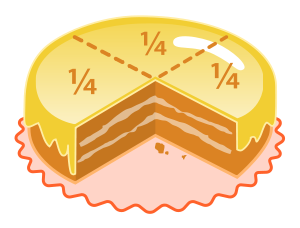
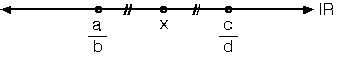A bir tam sayı B sıfırdan farklı bir tam sayı olmak üzere A/B şeklinde yazılabilen sayılara rasyonel sayılar denir.Payda sıfır olursa tanımsız olur.Rasyonel sayılar Q sembolü ile gösterilir.
Her tam sayı aslında bir rasyonel sayıdır. Çünkü her tam sayının altında gizli 1 vardır.Bunu açığa çıkartınca sayı rasyonel sayıya dönüşür.
N: Doğal sayılar, Z: Tam sayılar, Q: Rasyonel sayılar
Ondalık kesirler ve devirli ondalık açılımlar birer rasyonel sayıdır.
Basit Kesir: Payı küçük paydası büyük olan kesirlerdir.
Bileşik Kesir: Payı büyük paydası küçük olan kesirlerdir.Pay ve paydası aynı olan kesirlerde bileşik kesirdir.
Tamsayılı Kesir: Bir sayma sayısı ve bir basit kesir ile birlikte yazılan kesirlerdir.Her bileşik kesir aynı zamanda tamsayılı kesirdir.
Bileşik kesirler tam sayılı kesre çevrilirken;
Pay paydaya bölünür.Bölüm tam sayı,kalan pay,bölen payda olarak yazılır.
Rasyonel Sayıların Sayı Doğrusunda Gösterilmesi:
Pozitif işaretli basit kesirler sayı doğrusunda her zaman 0 ile 1 arasında gösterilir.
Negatif işaretli basit kesirler sayı doğrusunda her zaman -1 ile 0 arasında gösterilir.
Bileşik kesirler sayı doğrusunda gösterilmeden önce tam sayılı kesre dönüştürülür.Tam sayılı kesre sıfırdan başlayarak tam sayı kadar yol aldırılır.Daha sonra şu yol izlenir.Bir sonraki tam sayıya kadar olan aralık,tamsayının yanındaki kesrin paydası kadar parçalanarak pay kadar yol aldırılır.
Rasyonel Sayılarda Sıralama:
Pozitif rasyonel sayılarda sıralama yaparken paydalar eşitlenir,payı büyük olan büyüktür.
Pozitif rasyonel sayılarda sıralama yaparken paylar eşitlenirse,paydası büyük olan küçüktür.
Negatif rasyonel sayılarda sıralama yaparken, pozitif rasyonel sayılardaki gibi sıralama yapılır.Sonra sıralamanın tam tersi alınır.
Negatif ve pozitif rasyonel sayılar karışık verilirse yine payda eşitlenir.Negatif olanların daima küçük,pozitif olanların daima büyük olduğu unutulmamalıdır.
Rasyonel sayıları sıralarken sayı doğrusuna da kullanabiliriz.Sağdan kalanlar hep büyük olur,solda kalanlar hep küçük olur.
Rasyonel Sayılarda Toplama ve Çıkarma İşlemleri
Rasyonel sayılarda toplama ve çıkarma işlemlerini yapabilmek için paydaları eşitlememiz gerekir.Paydalar eşitlendikten sonra paylar toplanır veya çıkarılır,payda ortak payda olarak yazılır.
Rasyonel Sayılarda Çarpma ve Bölme İşlemleri
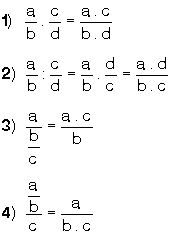
Rasyonel sayılarda çarpma işlemini yaparken payla pay,paydayla payda çarpılır.
Rasyonel sayılarda bölme işlemini yaparken 1.kesrimiz aynen yazılır, 2. kesrimiz ters çevrilip ilk kesirle çarpılır.
A. TANIM
a ve b tam sayı, b ¹ 0 olmak üzere, şeklinde ifade edilen sayılara rasyonel sayı veya kesir denir.
Pay
Kesir cizgisi
Payda
| · |  |
| · |
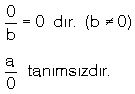B. KESİR ÇEŞİTLERİ
1. Basit Kesir
İşaretine bakılmaksızın payı paydasından küçük olan kesirlere basit kesir denir.
-
basit kesir ise 
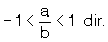
- pozitif basit kesir ise ;
2. Bileşik Kesir
İşaretine bakılmaksızın payı paydasından küçük olmayan (büyük veya eşit olan) kesirlere bileşik kesir denir.
- bileşik kesir ise,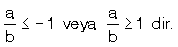
3. Tam sayılı Kesir
Herhangi bir sayma sayısı ile birlikte yazılabilen kesirlere tam sayılı kesir denir.
Her bileşik kesir bir tamsayılı kesir biçiminde yazılabilir.
C. RASYONEL SAYILARDA İŞLEMLER
1. Genişletme ve Sadeleştirme
k ¹ 0 olmak üzere,
2. Toplama - Çıkarma
Toplama ve çıkarma işleminde payda eşitlenecek biçimde kesirler genişletilir ya da sadeleştirilir. Oluşan kesirlerin payları toplanır (ya da çıkarılır) ortak payda alınır.
3.Çarpma -Bölme
4. İşlem Önceliği
Toplama, çıkarma, çarpma, bölme ve üs alma işlemlerinden bir kaçının birlikte bulunduğu rasyonel sayılarda işlemler, aşağıdaki sıraya göre yapılır.
- Parantezler ve kesir çizgisi işleme yön verir.
- Üslü işlemler varsa sonuçlandırılır.
- Çarpma - bölme yapılır.
- Toplama - çıkarma yapılır.
| Toplama ile çıkarma ve çarpma ile bölme kendi arasında öncelik taşımaz. Özellikle çarpma ile bölmede öncelik söz konusu ise bu, parantezle belirlenir. |
D. ONDALIKLI SAYILAR
1. Ondalıklı Sayı
a bir tam sayı ve n bir sayma sayısı ise
biçimindeki rasyonel sayılara ondalıklı sayı denir.
Burada a ya tam kısım, bcd ye de ondalıklı kısım denir.
2. Devirli (Periyodik) Ondalıklı Sayı
Bir ondalıklı sayıda ondalıklı kısım belli bir kurala göre tekrarlanıyorsa bu sayıya devirli ondalıklı sayı denir.
Devreden kısım üzerine (—) işareti konulur.
a,bcbcbc ... = a, bc dir.
3. Ondalık Sayılarda İşlemler
a. Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama - çıkarma işleminde olduğu gibi toplama - çıkarma işlemi yapılır. Sonuç, virgüllerin hizasından virgülle ayrılır.
b. Çarpma: Ondalık kesirlerin çarpımı yapılırken, virgül yokmuş gibi çarpma işlemi yapılır. Sonuç, çarpılan sayıların virgülden sonraki basamak sayılarının toplamı kadar, sağdan sola doğru virgülle ayrılır.
c. Bölme: Ondalık kesirlerin bölme işlemi yapılırken, bölen virgülden kurtulacak biçimde 10 un kuvveti ile çarpılır. Bölen de aynı 10 un kuvveti ile çarpılarak normal bölme işlemi yapılır.
4. Devirli Ondalık Sayıların Rasyonel Sayıya Dönüştürülmesi
Tüm sayı - Devretmeyen sayı
Verilen sayı=
Devreden rakam sayısı kadar 9devretmeyen
kadar rakam sayısı kadar 0(sıfır)
Devreden 9 ise bir önceki rakam 1 artırılır.
3,9 =4; 3,59 =3,6 dir.
E. RASYONEL SAYILARDA SIRALAMA
Pozitif kesirlerde sıralama yapılırken aşağıdaki yollardan biri kullanılır.
I. Yol:
Paydaları eşit olan (eşitlenen) kesirlerden payı en büyük olan diğerlerinden daha büyüktür.
II. Yol:
Payları eşit olan (eşitlenen) kesirlerden paydası en küçük olan diğerlerinden daha büyüktür.
III. Yol:
Payı ile paydası arasındaki farkı eşit olan, basit kesirlerde, payı en büyük olan diğerlerinden daha büyüktür.
Payı ile paydası arasındaki farkı eşit olan, bileşik kesirlerde, payı en büyük olan diğerlerinden daha küçüktür.
Yukarıda verilen yöntemler pozitif kesirlerde geçerlidir. Negatif kesirlerde ise durum tersinedir.
F. İKİ RASYONEL SAYI ARASINDAKİ SAYILAR
arasında sayılamayacak çoklukta rasyonel sayı vardır. Bunlardan bazılarını bulmak için b ile d nin OKEK i bulunur. Verilen kesirlerin paydaları bulunan OKEK inde eşitlenir. İstenen koşuldaki sayıyı bulmak için kesirler genişletilebilir.
| Ü | x, kesirlerinin ortasındaki bir sayı ise, |
