Türkçe Bilgi: dört yüzlü

tetrahedron veya dörtyüzlü, dört üçgen yüzden oluşan bir çokyüzlüdür (polihedron), her köşesinde üç üçgen birleşir. Düzgün dörtyüzlü dört üçgenin eşkenar olduğu bir dörtyüzlüdür ve Platonik cisimlerden biridir. Dörtyüzlü, dört yüzü olan tek konveks çokyüzlüdür. Tetrahedron isminin sıfat hali (tetrahedrona ait veya tetrahedronla ilişkili anlamında) "tetrahedral"dir. Dörtyüzlü, simpleks kavramının üç boyutlu halidir. Dörtyüzlü, bir cins piramittir. Piramit, çokgen bir tabanı tek bir noktada birleştiren üçgen yüzlerden oluşur. Dörtyüzlü durumunda taban bir üçgendir (dört yüzün herhangi biri taban sayılabilir), dolayısıyla dörtyüzlü ayrıca üçgen piramit olarak da bilinir. Tüm dışbükey (konveks) çokgenler gibi, dörtyüzlü de tek bir kağıt yaprağın katlanması ile meydana gelebilir. İki ağ oluşur. |align=center|

A=4\,A_0=}a^2 \,

|- |Yükseklik |align=center|

\sqrt\,a \,

|- |Hacim Kenarlar arasındaki uzaklık Dörtyüzlünün iki karşı kenarı, iki aykırı doğru üzerinde yer alırlar (aykırı doğrular birbirlerine ne paralel ne de birbirini kesen doğrulardır). Bu iki doğru arasındaki en yakın noktalar kenarlara ait noktalarsa bu noktalar kenarlar arasındaki en yakın uzaklığı tanımlar; aksi halde, kenarlar arasındaki uzaklık, uç noktalar ve karşı kenar arasındaki uzaklıklardan en kısa olanıdır. a ve b-c karşı kenarlarının oluşturduğu aykırı doğrular arasındaki uzaklık

d

olsun. Bu durumda hacim için bir diğer formül şöyledir: :

V = \frac  \times \mathbf)| } .

Geometrik ilişkiler . (50-70 cm tam çözünürlükte izlenmesi önerilir) ]] Dörtyüzlü bir 3-simpleks'tir. Diğer Platonik cisimlerden farklı olarak, bir düzgün dörtyüzlünün tüm köşeleri birbirinden eşit uzaklıktadır. Köşeler, üç boyutlu uzayda dört noktanın birbirine eşit uzaklıkta olabileceği tek konumdadır. Dörtyüzlü, üçgensel bir piramittir. Düzgün dörtyüzlü öz-çifteş (İng. self-dual). Düzgün bir dörtyüzlü bir küpün içine iki farklı şekilde yerleştirilebilir, her köşe küpün bir köşesi ve her kenar küpün yüzlerinden birinin çaprazı olacak şekilde. Bu yerleştirmelerden biri için, köşelerin koordinatları şöyledir: : (+1, +1, +1); : (−1, −1, +1); : (−1, +1, −1); : (+1, −1, −1). Meydana gelen bu dörtyüzlünün orijin merkezli olup kenar uzunluğu 2√2'dir. Öbür dörtyüzlü (birincisinin öz-çifteşidir) için tüm işaretlerin tersini alın. Bu iki dörtyüzlünün köşeleri birlikte küpün köşelerini meydana getirirler. Böylece bir düzgün dörtyüzlünün bir 3-yarıküpü (3-demicube) olduğu gösterilmiş olur. Bu dörtyüzlünün hacmi kübün hacminin 1/3'üdür. İki dörtyüzlüyü birleştirince bir birleşik çokyüzlü (aynı merkeze sahip birden çok çokyüzlü) oluşur, bunun adı iki dörtyüzlü bileşimi (compound of two tetrahedra) veya yıldızlaşmış sekizyüzlü (stellated octahedron)'dur. Yıldızlaşmış sekizyüzlünün içi bir sekizyüzlüdür. Dolayısıyla, düzgün bir dörtyüzlüden yarım kenar uzunluğunda dört tane düzgün dörtyüzlü kesilmesinin sonucu, düzgün bir sekizyüzlüdür. Bu işleme dörtyüzlünün rektifikasyonu denir. Küpün içine bir dörtyüzlü yerleştirince beş dörtyüzlü meydana gelir, bunlardan biri düzgündür. Bir küpü oluşturmak için gereken dörtyüzlü sayısı en az 5'tir. Düzgün çokyüzlüler uzayı karolayamazlar. Bunun olabileceği o kadar makul görünmüştür ki Aristo bunun olabileceğini iddia etmiştir. Ancak, iki düzgün dörtyüzlü ve bir sekizyüzlü ile birleştirilerek bir eşaltıyüzlü (rhombohedron) oluşur, bununla uzay karolanabilir. Ancak, uzayın karolayabilen en az bir düzensiz dörtyüzlü vardır. Dörtyüzlülerin hepsinin aynı boyda olması şartı esnetilirse, sadece dörtyüzlüler kullanarak uzayı kaplamak mümkündür. Örneğin bir sekizyüzlüyü dört döryüzlüye bölüp bunları iki düzgün dörtyüzlü ile birleştirilebilir (bu iki tip dörtyüzlünün hacimleri eşittir). Düzgün çokyüzlüler arasında paralel yüzlere sahip olmayan tek cisim dörtyüzlüdür.

İlgili çokyüzlüler

Dosya:Truncatedtetrahedron.jpg|Kesik dörtyüzlü Dosya:Stella-octangula-in-cube.png|bir küp içinde iki dörtyüzlü Dosya:Compound of five tetrahedra.png|Beş dörtyülü bileşimi Dosya:Compound of ten tetrahedra.png|On dörtyüzlü bileşimi Bir dörtyüzlüye uygulanacak bir kesme işlemi düzgün bir çokyüzlüler serisi meydana getirir. Kalan kenarları nokta haline getirecek şekilde kesmek, rektifiye bir dörtyüzlü olan bir sekizyüzlü oluşturur. Bu işlem devam ettirilirse sonunda ikili rektifikasyon (birectification) olur, başlangıçtaki yüzler birer noktaya indirgenir, ve öz-çifteş dörtyüzlü yeni baştan ortaya çıkar.

Kesişen dörtyüzlüler

Kesişen beş tane dörtyüzlü ile ilginç bir çokyüzlü inşa edilebilir. Beş tane dörtlüden oluşan bu bileşik yüzyıllardır bilinmektedir. Origamide sık sık görülür. 20 köşenin birleştirilmesi ile bir dodekahedron (yirmiyüzlü) meydana gelir. Birbirinin ayna görüntüsü olan sağ elli ve sol elli biçimleri vardır. ==IzometriDüzgün dörtyüzlerde izometriler Bir küpün köşeleri, her biri bir dörtyüzlü oluşturan, dörtlü iki gruba ayrılabilir (bkz. yukarısı, ve ayrıca ). Düzgün bir dörtyüzlünün simetrileri bir kübün simetrilerinin yarısına karşılık gelir: dörtyüzlüleri kendilerine dönüştürenler ve birbirine dönüştürmeyenler. Dörtyüzlü, platonik cisimler arasında noktasal yansıma ile kendi kendine rastlamayan tek cisimdir. Düzgün dörtyüzlünün 24 izometrisi vardır, T_d simetri grubu ve ona eşbiçimli(izomorfik) olan S₄ oluşturur. Bunlar şöyle kategorilendirilebilir: *T, A₄ almaşık grubu (özdeşlik ve 11 dönme işlemi) ile izomorfiktir, aşağıdaki eşlenik sınıfları vardır (parantez içinde köşelerin permutasyonları ve birim kuaterniyon gösterimleri verilmiştir): **özdeşlik **bir köşeden geçen ve karşı yüze dik bir eksen etrafında ±120° dönme: 4 eksen, eksen başına 2, birlikte 8((123), vb.; (1±i±j±k)/2) ** 180° bir açıyla dönme öyleki kenar karşı kenar ile çakışsın. 3 ((1 2)(3 4), vb.; i,j,k) *bir kenara dik bir düzlemde yansıma: 6 *bir düzlemde yansıma ile o düzleme dik bir eksen etrafında 90° dönme: 3 eksen, eksen başına 2, birlikte 6; buna eşdeğer olarak, 90° dönmelerle ters dönmeler (xin −xe dönüşmesi) birleşimidir: dönmeler bir küpte bir yüzü öbür yüze dönüştüren dönmelere karşılık gelir.

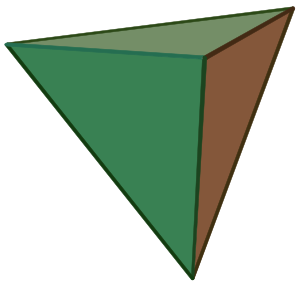
Düzensiz dörtyüzlülerin izometrileri

Düzensiz bir dörtyüzlünün izometrileri (eşölçer dönüşümleri) dörtyüzlünün geometrisine bağlıdır, 7 durum olabilir. Her durumda bir 3-boyutlu noktalar kümesi meydana gelir. * Eşkenar üçgen bir taban ve (eşkenar olmayan) ikizkenar üçgen kenarlar durumunda 6 izometri vardır, bunlara tabanın 6 izometrisine karşılık gelir. Köşelerin permutasyonlarına karşılık gelen bu 6 izometri şunlardır: özdeşlik 1, (123), (132), (12), (13) ve (23). Bunlar S₃ ile izomorfik olan C_3vsimetri grubunu oluşturur. * Dört (eşkenar olmayan) ikizkenar üçgen 8 izometri verir. Eğer (1,2) ve (3,4) kenarları diğer dört kenradan farklı uzunluktaysa bu 8 izometri şunlardır: özdeşlik 1, yansımalar (12) ve (34), ve 180° dönmeler (12)(34), (13)(24), (14)(23) ve 90° dönmeleri (1234) and (1432). Bunlar D_2d simetir grubunu oluşturur. * Dört çeşitlenar üçgen 4 izometri verir. İzometriler şunlardır: 1 ve 180° dönmeleri (12)(34), (13)(24) ve (14)(23). Bu, Klein dört-kümesi V₄ ≅ Z₂² (nokta kümesi D₂ olan). * İki çift izomorfik (eşkenar olmayan) ikizkenar üçgen. Birbirine dik ve farklı uzunlukta (1,2) and (3,4) kenarları vardır. 4 izometeriler şunlardır: 1, yansıma (12) ve (34) ve 180° dönmeleri (12)(34). Simetri grubu C_2vdır, V₄e izomorfiktir. * İki çift izomofik çeşitkenar üçgen. İki çift eşit uzunluklu kenar vardır (1,3), (2,4) ve (1,4), (2,3) ama bunlar dışında hiçbir kenar eşit değildir. Olan izometriler 1 ve (12)(34) dönmesidir. Simetri grubu C₂dır, Z₂e izomorfiktir. *Ortak kenarlı iki farklı eşkenar üçgen. İki çift eşit uzunluklu kenarlar vardır (1,3), (1,4) ve (2,3), (2,4), ama bunlar dışında hiçbir kenar eşit değildir. Olan izometriler 1 ve (34) yansımasıdır. Simetri grubu C_sdır, Z₂e izomorfiktir. *Hiç bir kenar birbirine eşit değildir, tek izometri özdeşliktir ve simetri grubu trivial gruptur. == Dörtyüzlüler için sinüsler kanunu ve tüm dörtyüzlü şekillerinin uzayı== Sinüs teoreminin bir sonucu olarak, köşeleri O, A, B, C olan bir dörtyüzlüde :

\sin\angle OAB\cdot\sin\angle OBC\cdot\sin\angle OCA = \sin\angle OAC\cdot\sin\angle OCB\cdot\sin\angle OBA.\,

Bu eşitliğin iki tarafı, yüzlerin saat yönlü ve ters saat yönlü okunuşu gibi düşünülebilir. Dört köşeden her birini O köşesi yerine koymak buna benzer dört eşitlik yaratır, ama bunların en fazla üç tanesi bağımsızdır: eğer eşitliklerin "saat yönlü" tarafları birbiriyle çarpılırsa, sonucun "ters saat yönlü" tarafların çarpımına eşit olduğu çıkarımı yapılabilir. Her iki taraftaki ortak çarpanlar atılırsa geriye kalan, dördüncü eşitliktir. Bu "bağımsızlık" ilişkisinin önemli olmasının bir nedeni şudur: üç açının bir üçgene ait olması için toplamlarının yarım çembere (180°) eşit olması gerekir. 12 açı için hangi şart bunların bir dörtyüzlüye ait olmasını sağlar? Dörtyüzlünün her bir yüzündeki açıların toplamı yarım çemberdir. Bu şekilde dört üçgen olduğuna göre açı toplamlarına etki eden dört kısıt vardır. Dolayısıyla serbestlik derecesi 12'den 8'e düşer. Bu sinüs teoreminindeki dört ilişki, serbestlik derecelerini 8'den 4'e değil, 5'e indirir, çünkü dördüncü kısıt ilk üçten bağımsız değildir. Dolayısıyla olasıl tüm dörtyüzlülerin oluşturduğu açı değerlerinin uzayı 5 boyutludur. == Uygulamalar ==

Sayısal analiz

de, özellikle kısmi diferansiyel denklemlerin sayısal çözümlerinde, sonlu eleman analizi için denklemler kurarken, karmaşık üç boyutlu şekiller çoğu zaman düzensiz dörtyüzlülerden oluşan bir çokgen ağ ile yaklaşıklanır. Bu yöntemler çeşitli mühendislik dallarında yaygın olarak kullanılmaktadır.

Kimya

da kuaterner faz diyagramları grafik olarak tetrahedron olarak gösterilir. (Ancak, iletişim mühendisliğinde kuaterner faz diyagramları grafik olarak iki boyutlu gösterilir.)

Elektrik ve elektronik

Eğer dört eşit rezistör birbirine bağlanarak bir tetrahedron oluşturursa, iki köşe arasındaki direnç, bir rezistörün direncinin yarısı kadardır.

Oyun

Özellikle rol oyunlarında dört-yüzlü zar sık kullanılır. Atılan sayı ya tabanın etrafında ya da üst köşede yazılı olur. Bazı Rubik Küpü-benzeri bulmacalar dörtyüzlüdür, örneğin Pyraminx ve Pyramorphix.

Renk uzayı

dönüşüm algoritmalarında, özellikle lüminans ekseni renk uzayını çapraz kestiği durumlarda (örneğin RGB, CMY), tetrahedral interpolasyon kullanılır.

Jeoloji

William Lowthian Green tarafından ilk yayımlanan ve Dünyanın oluşumunu açıklamak için öne sürülen tetrahedral hypotez, 20. yüzyılın başlarında popülerdi. == Doğada

Kimya

Dörtyüzlü (tetrahedron) şekli, moleküllerin kovalent bağlarında görülür. sp³-hibritlenmiş atomlara çevreleyen atomlar bir dörtyüzlünün köşelerinde yer alır, yani tetrahedral moleküler geometriye sahiptir. Örneğin, bir metan molekülü (CH₄) veya bir amonyak iyonunda (NH₄⁺), merkezdeki karbon veya azot atomu, tetrahedral simetriye sahip dört hidrojen atomu ile çevrilidir. Bu yüzden organik kimyanın önde gelen dergilerinden biri Tetrahedron olarak adlandırılmıştır. Düzgün bir dörtyüzlünün iki köşesi arasındaki merkez açı θ =

\arccos\right)}

, veya yaklaşık 109.47°'dir. Elektronikte kullanılan en yaygın yarı iletken olan silikonun değerlik sayısı dörttür. Silikon atomunun bağlarının tetrahedral şekli, silikon kristallerinin oluşumunu ve şekillerini belirler. Kaynakça Ayrıca bakınız * Dörtyüzlüsel sayı * Tetra Pak

Dört Yüzlü

İlgili çokyüzlüler

Kesişen dörtyüzlüler

Düzensiz dörtyüzlülerin izometrileri

Sayısal analiz

Sayısal analiz

Kimya

Kimya

Elektrik ve elektronik

Oyun

Renk uzayı

Renk uzayı

Jeoloji

Kimya

Dört yüzlü

Siyah yüzlü impala

Sekiz yüzlü

Erik yüzlü lori

Bebek Yüzlü

Platonik cisim

Sarı yüzlü iskete

Thomisus onustus

Dört Yüzlü

Dört Yüzlü Hakkında Detaylı Bilgi

İlgili çokyüzlüler

Kesişen dörtyüzlüler

Düzensiz dörtyüzlülerin izometrileri

Sayısal analiz

Sayısal analiz

Kimya

Kimya

Elektrik ve elektronik

Oyun

Renk uzayı

Renk uzayı

Jeoloji

Kimya

Görüşler ve Yorumlar

Okuma Önerileri

Dört yüzlü

Siyah yüzlü impala

Sekiz yüzlü

Erik yüzlü lori

Bebek Yüzlü

Platonik cisim

Sarı yüzlü iskete

Thomisus onustus