Kepler'in Gezegensel Hareket Yasaları
Kısaca: Kepler'in gezegensel hareket yasaları, Güneş Sisteminde bulunan gezegenlerin hareketlerini açıklayan üç matematiksel yasadır. Alman matematikçisi ve astronomu Johannes Kepler (1572-1630) tarafından keşfedilmişlerdir. ...devamı ☟
Kepler'in gezegensel hareket yasaları Resimleri



Johannes Kepler
3 yıl önceadlı çalışmalarına bağlı olarak, şahsen ortaya çıkardığı Kepler'in gezegensel hareket yasaları ile tanınır. Bu çalışmalar Isaac Newton’un evrensel yerçekimi...
Johannes Kepler, 1571, 1591, 1596, 1598, 15 Kasım, 1606, 1609, 1619, 1626, 1627Yörünge mekaniği
3 yıl öncekuralları kullanır. Matematiksel Newton yasaları kullanılarak elde edilebilen Kepler'in gezegensel hareket yasaları, sadece sigara yerçekimi kuvvetleri yokluğunda...
Kepler Yörüngesi
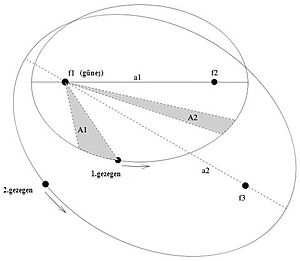
3 yıl öncegözlemlerini sığdırmaya çalışarak geçirecekti. 1609 yılında Kepler gezegensel hareketin üç yasasından ilk ikisini yayınladı. Birinci yasası: “Her gezegenin...
Kutupsal koordinat sistemi
3 yıl öncevazgeçilmiştir. Kutupsal koordinatlar, Kepler'in gezegensel hareket kanunları için doğal bir ifade yöntemi sağlar. Kepler'in birinci kanununa göre, bir yıldız...
Kutupsal koordinat sistemi, Kutupsal koordinat sistemi, 1625, 1647, 1816, Akışkan, Antik Yunan uygarlığı, Arşimet, Açı, Açısal momentum, Blaise PascalKütle
3 yıl öncegözlemlerini kullanarak, Kepler, gezegensel hareketi karakterize etmek için kendi yöntemini geliştirmek adına 5 yıl çalıştı. 1609’da Kepler, gezegenlerin Güneş...
Kütle, Fizik, Görelilik teorisi, Kimya, Madde, Parçacık fiziği, SI birim sistemi, Taslak, ElektronVoltGezegen
3 yıl öncebünyesinde barındıran bir gezegensel model öne sürdü ve söz konusu durumun yıldızların görünür bir şekilde batıya doğru hareket etmesinden ötürü gerçekleştiğini...
Gezegen, 1 Ceres, 2003UB313, 90377 Sedna, Arapça, Asteroit, Astroloji, Ay (uydu), Cüce Gezegen, Dünya, Eski YunanEğik yörünge
7 yıl öncecisimlerin (Güneş, Ay) çekim etkileri ile, dışarıya doğru küçük bir eliptik hareket yaptığı gözlenir. Çekim etkisi biriktikçe kuzey-güney yönelimli bir analemma...
Edmond Halley
3 yıl öncegözlemleri ile geçirmesine rağmen yer çekimi ile de ilgilendi. Kepler'in gezegensel hareket yasaları'nın kanıtlanması kafasını kurcalayan bir problem idi. Ağustos...
Edmond Halley, 1406, 14 Ocak, 1531, 1656, 1673, 1675, 1676, 1678, 1682, 1684